The pbeFoam solver is a zero-dimensional solver code that solves a population balance equation in a single computational cell. This is equivalent to assume the system under examination is perfectly mixed, and no flow motion is considered. The objective of the solver is to allow kernels for the population balance equation to be rapidly tested, and their prediction compared to either experimental results or other computational studies for verification and validation purposes.
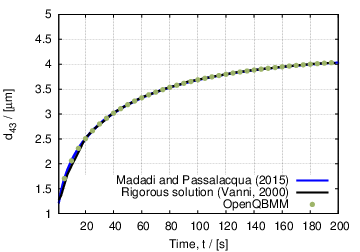
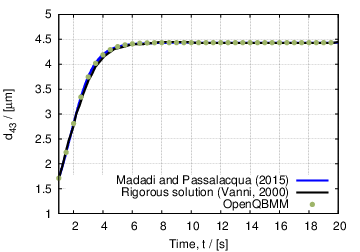
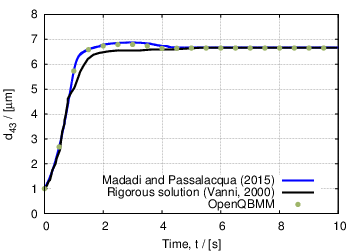
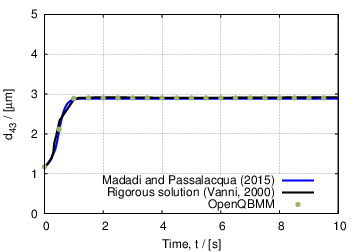
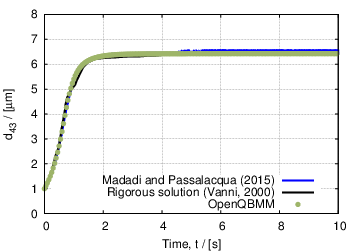
We will show here the predicitions of pbeFoam in comparison to the rigorous solution of the population balance equation from Vanni (2000), and with the numerical solution obtained with another code by Madadi and Passalacqua (2015) using the extended quadrature method of moments (EQMOM) (Yuan et al., 2012). On one hand, the comparison of the two numerical solution, the one obtained with OpenQBMM and the one from Madadi and Passalacqua (2015) serves as verification of the code, since both the data are obtained with the EQMOM procedure, using log-normal kernel density functions. On the other hand, the comparison between the OpenQBMM predictions and the rigorous solution of Vanni (2000) provides a validation of the implementation and of the numerical procedure.
Cases
The five cases reported in Madadi and Passalacqua (2015) were considered. The input files and the scripts to repeat this verification and validation study are provided with the OpenQBMM code, and are contained in the OpenQBMM/validation/madadiPassalacquaLognormal directory. For consistency with the numbering used in the reference of Madadi and Passalacqua (2015), we number cases from 5 to 9.
The following table summarizes the aggregation, breakup and daughter distribution function kernels used in each case:
| Case | Aggregation kernel | Breakup kernel | Daughter distribution |
| 5 | Constant | Constant | Symmetric fragmentation |
| 6 | Sum | Power law | Symmetric fragmentation |
| 7 | Hydrodynamic | Exponential | Symmetric fragmentation |
| 8 | Differential force | Power law | Uniform |
| 9 | Hydrodynamic | Exponential | One quarter mass ratio |
Results
The time evolution of the mean particle size, calculated as d43 = m4/m3, where m3 and m4 are the third- and fourth-order moment of the number density function describing the particle size distribution, are reported below. The blue line represents the numerical solution obtained by Madadi and Passalacqua (2015), the black line is the rigorous solution from Vanni (2000), and the green dots are the prediction obtained with the EQMOM with log-normal kernel density functions available in OpenQBMM.
Fig. 1: Time-evolution of d43 in case 5.
Fig. 2: Time evolution of d43 for case 6.
Fig. 3: Time evolution of d43 for case 7.
Fig. 4: Time evolution of d43 for case 8.
Fig. 5: Time evolution of d43 for case 9.